Magic Squares
Magic squares are fascinating mathematical objects that have been studied for centuries. A magic square is an arrangement of numbers in a square grid, where the numbers in each row, column, and diagonal add up to the same constant value. This constant sum is called the "magic constant."
Here are a few key properties of magic squares:
Square Grid: A magic square is always a square grid, meaning it has the same number of rows as columns. Common examples include 3x3, 4x4, 5x5, and so on.
Magic Constant: The magic constant is determined by the size of the square. For a standard 3x3 magic square, the magic constant is 15. For a 4x4 magic square, the magic constant is 34. In general, for an n x n magic square, the magic constant is given by the formula n(n^2 + 1) / 2.
Unique Numbers: Each number from 1 to n^2 is used exactly once in a magic square. In a 3x3 magic square, the numbers 1 to 9 are used once each.
Symmetry: Magic squares often exhibit various forms of symmetry. For example, reflectional symmetry can be found in many magic squares, where swapping rows or columns produces an equivalent square.
Methods of Construction: There are different methods to construct magic squares. The most well-known method is the Siamese method, also known as the De la Loubère's method, for constructing odd-sized magic squares. There are also algorithms and formulas for constructing magic squares of even sizes.
Magic squares have captured the attention of mathematicians, puzzle enthusiasts, and even artists throughout history. They continue to be an intriguing area of study, with ongoing research focused on understanding their properties and discovering new variations.
Number Sequences
Number sequences are ordered lists of numbers that follow a specific pattern or rule. These sequences can be finite or infinite and are often studied in mathematics, where they play a fundamental role in various branches, including number theory and analysis. Here are a few common types of number sequences:
Arithmetic Sequence: In an arithmetic sequence, each term is obtained by adding a constant value called the common difference to the previous term. For example, 2, 5, 8, 11, 14 is an arithmetic sequence with a common difference of 3.
Geometric Sequence: In a geometric sequence, each term is obtained by multiplying the previous term by a constant value called the common ratio. For example, 3, 6, 12, 24, 48 is a geometric sequence with a common ratio of 2.
Fibonacci Sequence: The Fibonacci sequence is a famous sequence where each term is the sum of the two preceding terms. It starts with 0 and 1, so the sequence begins as 0, 1, 1, 2, 3, 5, 8, 13, and so on.
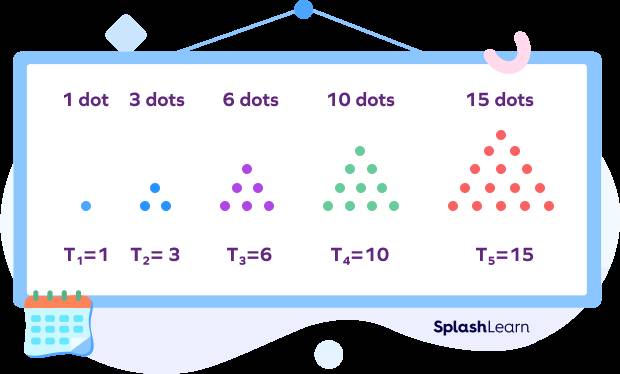
Triangular Numbers: Triangular numbers are generated by adding consecutive positive integers. The nth triangular number is the sum of the first n positive integers. For example, the sequence 1, 3, 6, 10, 15 represents the triangular numbers.
Prime Numbers: Prime numbers are numbers that are only divisible by 1 and themselves. The sequence of prime numbers begins as 2, 3, 5, 7, 11, 13, 17, and so on.
Square Numbers: Square numbers are obtained by squaring the positive integers. The sequence of square numbers starts with 1, 4, 9, 16, 25, 36, and so on.
These are just a few examples of number sequences, but there are countless others, each with its own distinct pattern or rule. Mathematicians study number sequences to understand the underlying structures, relationships, and properties they possess. Number sequences are also commonly used in puzzles, problem-solving, and real-life applications, such as in financial modeling or computer algorithms.



No comments yet
Be the first to share your thoughts!