Translational symmetry is a concept in mathematics and physics that describes a type of symmetry where an object or system remains unchanged when it is translated by a certain distance in a specific direction. In other words, if an object exhibits translational symmetry, it looks the same at different locations in space.
In mathematics, translational symmetry is often studied in the context of geometry and crystallography. In a geometric setting, a figure or shape possesses translational symmetry if it can be shifted or slid by a fixed amount in any direction and still appear identical. This means that if you move the shape horizontally, vertically, or diagonally by a particular distance, it will maintain its original form.
In crystallography, translational symmetry plays a crucial role in describing the regular and repeating arrangement of atoms or molecules in a crystal lattice. A crystal is characterized by its translational symmetry because the arrangement of atoms or molecules in the lattice is repeated throughout the crystal structure. This repetitive pattern allows for the prediction and understanding of various properties and behaviors of crystals, such as their optical, electrical, and mechanical properties.
In physics, translational symmetry is closely related to the concept of conservation of momentum. According to Noether's theorem, when a physical system exhibits translational symmetry, it implies the conservation of linear momentum. This means that if a system's properties or equations of motion remain unchanged under translations, the total momentum of the system will be conserved.
Overall, translational symmetry is a fundamental concept in mathematics and physics, providing insights into the regularity and invariance of objects and systems under translations in space. It is an important tool for analyzing and understanding various phenomena in different fields of study.
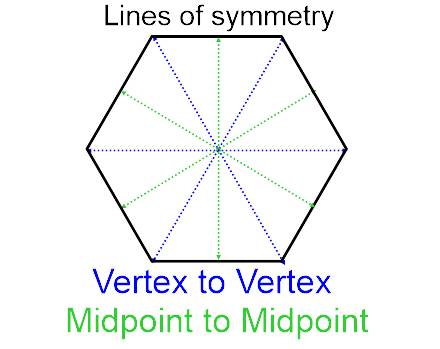
Polygons & Symmetry
Polygons and symmetry
Polygons and symmetry are closely related concepts in geometry. A polygon is a closed figure with straight sides that are connected to form a shape. Symmetry refers to a balanced arrangement of parts or elements on either side of a dividing line or center point.
There are several types of symmetry that can be observed in polygons:
Line Symmetry (or Reflection Symmetry): A polygon has line symmetry if there is a line, called the line of symmetry, such that one half of the polygon is a mirror image of the other half. For example, a square has four lines of symmetry, one for each side.
Point Symmetry (or Rotational Symmetry): A polygon has point symmetry if it can be rotated by a certain angle (usually less than a full turn) around a central point and still appear unchanged. Regular polygons, such as equilateral triangles, squares, and hexagons, have point symmetry.
Rotational Symmetry: A polygon has rotational symmetry if it can be rotated by a certain angle (usually less than a full turn) around a center point and still look the same in multiple positions. The number of distinct positions in which a polygon looks the same after rotation is called its rotational symmetry order. Regular polygons have rotational symmetry.
Glide Symmetry: Glide symmetry occurs when a polygon has both a line of symmetry and a translation symmetry. This means that the polygon can be reflected across a line of symmetry and then translated parallel to that line without changing its appearance.
Symmetry is an important concept in geometry as it helps us identify and analyze properties of shapes. It is often used in design, architecture, and various fields of science.
blogpay
Total Comments: 0