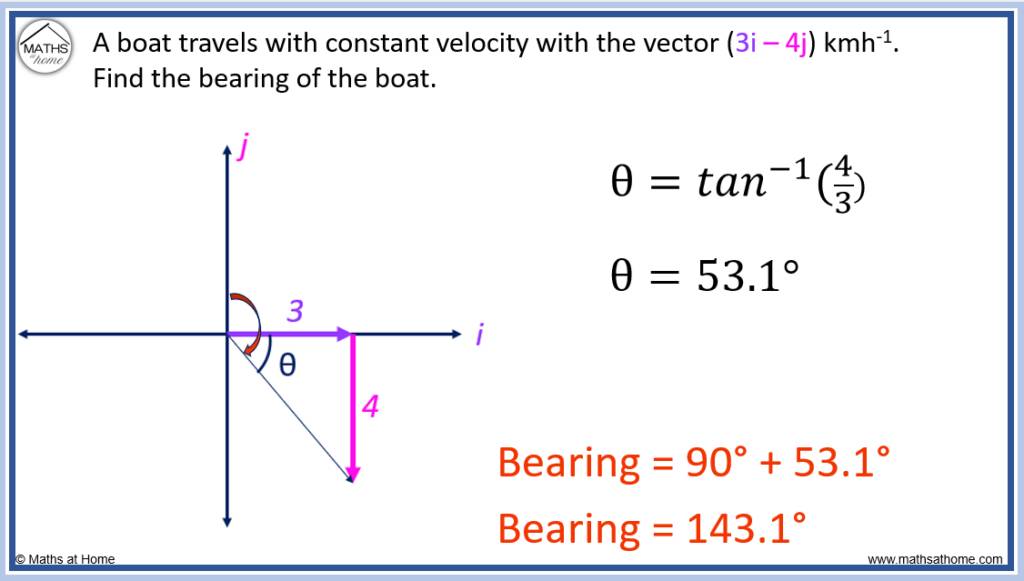
Bearings & Vectors Connection
Bearings and vectors
Bearings and vectors are concepts used in mathematics and physics to describe the direction and magnitude of quantities. While they are related, they have different interpretations and uses.
Bearings: Bearings are used to describe directions in a horizontal plane, typically in navigation or engineering applications. Bearings are measured clockwise from a reference direction, usually the north direction. Bearings are often represented as angles, such as 0° for north, 90° for east, 180° for south, and 270° for west. Bearings can also be given in degrees and minutes, such as 45° 30'.
Vectors: Vectors are mathematical entities used to represent quantities that have both magnitude and direction. Vectors can describe various physical quantities, such as displacement, velocity, force, or acceleration. A vector is typically represented by an arrow, where the length of the arrow represents the magnitude of the vector, and the direction of the arrow represents the direction of the vector.
Vectors can be expressed in terms of their components, which are typically represented by Cartesian coordinates (x, y, z) in three-dimensional space. The components of a vector represent its projections along the x, y, and z axes. Vectors can also be represented in terms of magnitude and direction, often using trigonometric functions such as sine and cosine.
Both bearings and vectors are used in different contexts and have different interpretations, but they share the common aspect of representing directions. Bearings are specifically used for horizontal directions, while vectors are more general and can represent various quantities in both two-dimensional and three-dimensional space.
Bearings and vectors are concepts used in mathematics and physics to describe the direction and magnitude of quantities. While they are related, they have different interpretations and uses.
Bearings: Bearings are used to describe directions in a horizontal plane, typically in navigation or engineering applications. Bearings are measured clockwise from a reference direction, usually the north direction. Bearings are often represented as angles, such as 0° for north, 90° for east, 180° for south, and 270° for west. Bearings can also be given in degrees and minutes, such as 45° 30'.
Vectors: Vectors are mathematical entities used to represent quantities that have both magnitude and direction. Vectors can describe various physical quantities, such as displacement, velocity, force, or acceleration. A vector is typically represented by an arrow, where the length of the arrow represents the magnitude of the vector, and the direction of the arrow represents the direction of the vector.
Vectors can be expressed in terms of their components, which are typically represented by Cartesian coordinates (x, y, z) in three-dimensional space. The components of a vector represent its projections along the x, y, and z axes. Vectors can also be represented in terms of magnitude and direction, often using trigonometric functions such as sine and cosine.
Both bearings and vectors are used in different contexts and have different interpretations, but they share the common aspect of representing directions. Bearings are specifically used for horizontal directions, while vectors are more general and can represent various quantities in both two-dimensional and three-dimensional space.
Back bearings
Back bearings are related to bearings and are used in navigation and surveying. A back bearing is the opposite direction to a given bearing.
When navigating or surveying, a bearing is the direction from one point to another, typically measured clockwise from a reference direction, such as north. For example, if you are at point A and want to travel to point B, the bearing from A to B might be 45 degrees.
A back bearing, on the other hand, is the direction from the destination point back to the starting point. It is the opposite of the original bearing. In the example above, the back bearing from point B to point A would be 225 degrees (180 degrees + 45 degrees).
Back bearings can be useful in navigation and surveying to retrace a path or determine the bearing needed to return to the starting point. By taking the original bearing and adding 180 degrees (or subtracting 180 degrees if the bearing is already greater than 180 degrees), you can calculate the back bearing.
It's important to note that back bearings assume a straight line path between the two points and do not account for obstacles or changes in terrain. They are primarily used for initial planning or rough estimation and may need to be adjusted based on actual conditions.