### Understanding Logarithms: The Exponent Concept
A **logarithm** is a mathematical concept that answers the question: **To what power must a given base be raised to produce a specific number?** It is a fundamental tool in algebra, calculus, and many fields of science and engineering.
---
#### The Definition of a Logarithm
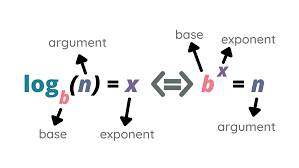
The logarithmic expression is written as:
\[
\log_b(y) = x
\]
This means that \( b^x = y \), where:
- \( b \) is the **base** (a positive number, \( b > 0 \), and \( b \neq 1 \)).
- \( y \) is the **result** or the number you're trying to reach.
- \( x \) is the **logarithm**, or the power/exponent to which the base \( b \) must be raised to produce \( y \).
---
#### Examples
1. \(\log_2(8) = 3\): Here, the base \( 2 \) must be raised to the power \( 3 \) to produce \( 8 \), since \( 2^3 = 8 \).
2. \(\log_{10}(1000) = 3\): The base \( 10 \) raised to \( 3 \) gives \( 1000 \), as \( 10^3 = 1000 \).
---
#### Types of Logarithms
1. **Common Logarithm (\( \log \))**:
- Base \( 10 \).
- Frequently used in science and engineering.
- Example: \(\log(1000) = 3\) (implies base 10).
2. **Natural Logarithm (\( \ln \))**:
- Base \( e \) (Euler's number, approximately \( 2.718 \)).
- Used in calculus and natural growth models.
- Example: \(\ln(e^2) = 2\).
3. **Binary Logarithm**:
- Base \( 2 \).
- Common in computer science and information theory.
- Example: \(\log_2(16) = 4\).
---
#### Properties of Logarithms
Logarithms have several important properties that simplify calculations:
1. **Product Rule**:
\[
\log_b(xy) = \log_b(x) + \log_b(y)
\]
2. **Quotient Rule**:
\[
\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)
\]
3. **Power Rule**:
\[
\log_b(x^k) = k \cdot \log_b(x)
\]
4. **Change of Base Formula**:
\[
\log_b(y) = \frac{\log_k(y)}{\log_k(b)}
\]
This allows you to convert logarithms to a more convenient base.
---
#### Applications of Logarithms
1. **Science**: Understanding phenomena that scale exponentially, such as sound intensity (decibels) or the pH scale in chemistry.
2. **Engineering**: Logarithms simplify complex multiplications into additions, useful in circuit design and signal processing.
3. **Computer Science**: Efficiently solving problems involving powers of two, such as data storage and algorithm complexity analysis.
4. **Finance**: Calculating compound interest and growth rates over time.
5. **Statistics**: Transforming data to manage skewed distributions.
---
#### Conclusion
Logarithms are powerful mathematical tools that connect exponential growth to linear functions. By providing a way to "reverse" exponentiation, they simplify many real-world problems involving multiplication, division, and scaling. Understanding logarithms is essential for mastering mathematics and applying it effectively in various scientific and practical domains.