### Understanding Logarithms: The Exponent Concept

A **logarithm** is a mathematical concept that answers the question: **To what power must a given base be raised to produce a specific number?** It is a fundamental tool in algebra, calculus, and many fields of science and engineering.

---

#### The Definition of a Logarithm

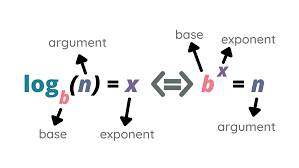
The logarithmic expression is written as:

\[

\log_b(y) = x

\]

This means that \( b^x = y \), where:

- \( b \) is the **base** (a positive number, \( b > 0 \), and \( b \neq 1 \)).

- \( y \) is the **result** or the number you're trying to reach.

- \( x \) is the **logarithm**, or the power/exponent to which the base \( b \) must be raised to produce \( y \).

---

#### Examples

1. \(\log_2(8) = 3\): Here, the base \( 2 \) must be raised to the power \( 3 \) to produce \( 8 \), since \( 2^3 = 8 \).

2. \(\log_{10}(1000) = 3\): The base \( 10 \) raised to \( 3 \) gives \( 1000 \), as \( 10^3 = 1000 \).

---

#### Types of Logarithms

1. **Common Logarithm (\( \log \))**:

   - Base \( 10 \).

   - Frequently used in science and engineering.

   - Example: \(\log(1000) = 3\) (implies base 10).

2. **Natural Logarithm (\( \ln \))**:

   - Base \( e \) (Euler's number, approximately \( 2.718 \)).

   - Used in calculus and natural growth models.

   - Example: \(\ln(e^2) = 2\).

3. **Binary Logarithm**:

   - Base \( 2 \).

   - Common in computer science and information theory.

   - Example: \(\log_2(16) = 4\).

---

#### Properties of Logarithms

Logarithms have several important properties that simplify calculations:

1. **Product Rule**:

   \[

   \log_b(xy) = \log_b(x) + \log_b(y)

   \]

2. **Quotient Rule**:

   \[

   \log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)

   \]

3. **Power Rule**:

   \[

   \log_b(x^k) = k \cdot \log_b(x)

   \]

4. **Change of Base Formula**:

   \[

   \log_b(y) = \frac{\log_k(y)}{\log_k(b)}

   \]

   This allows you to convert logarithms to a more convenient base.

---

#### Applications of Logarithms

1. **Science**: Understanding phenomena that scale exponentially, such as sound intensity (decibels) or the pH scale in chemistry.

2. **Engineering**: Logarithms simplify complex multiplications into additions, useful in circuit design and signal processing.

3. **Computer Science**: Efficiently solving problems involving powers of two, such as data storage and algorithm complexity analysis.

4. **Finance**: Calculating compound interest and growth rates over time.

5. **Statistics**: Transforming data to manage skewed distributions.

---

#### Conclusion

Logarithms are powerful mathematical tools that connect exponential growth to linear functions. By providing a way to "reverse" exponentiation, they simplify many real-world problems involving multiplication, division, and scaling. Understanding logarithms is essential for mastering mathematics and applying it effectively in various scientific and practical domains.

Meet the Author

View Profile

---

Kressman Osei

Content writer

follow me