ELECTIVE MATHEMATICS FOR SHS 1
BINARY OPERATIONS
Introduction
The word “binary” means composed of two units, components, elements, terms, parts or pieces. A binary operation is basically a rule for combining two values to create a new value.
Definition
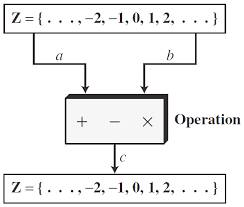
A binary operation is a rule that combines two elements of the same set to produce another element also of the set.
Symbols for Binary Operations
In a binary operation, mathematical symbols like ⊗, ⊕, ∆, ∇, ●, ■, ▲, * etc are used on the L.H.S. to join the inputs and defined at the R.H.S. in terms of mathematical operators like +, - , ÷ , ×.
Examples of a binary operations:
a ∆ b = a + b + 2ab
x ❍ y = x² – y²
m ⊕ n = mn... etc
Now lets do some calculations
Worked Examples
1. A binary operation is defined on the set of real numbers R, as follows:
a ⊗ b = a + b - ab. Evaluate;
a) 3 ⊗ 5
b) - 2 ⊗ - 3
Solution
a ⊗ b = a + b - ab.
a) 3 ⊗ 5 = 3 + 5 - (3)(5)
= 8 - 15
= - 7
b) - 2 ⊗ - 3
= (-2) + (-3) - (-2)(-3)
= - 5 - 6
= - 11
Now try the following
c) 1/2 ⊗ 1/3
2. Given that
x ∆ y = (x + y)(x - y)·
Evaluate a) 8 ∆ 5
b) √7 ∆ √3
c) 0.8 ∆ 0.5
Please do not forget to submit your solutions(or answers) before the next lesson.
Thank you.


Francisca
Mar 20, 2025More questions on e maths